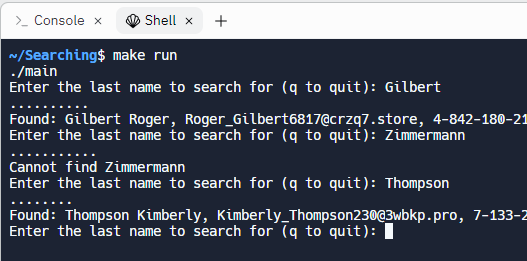
Searching Algorithms

Searching is a big part of everyday life today. When a friend asks, "Who was the actress who starred in the movie the Parent Trap?" you're accustomed to having the answer at your finger tips. Out comes your phone and you ask Siri or Google or DuckDuckGo. How do they know the answer? The programs search for it among all of the pages on the Internet. (Of course, even Google can be wrong; I've never heard of Lindsay Lohan. It's supposed to be Haley Mills!).
Searching Algorithms: the Big Picture
So, how does searching work? In this lesson, we'll look at two different techniques
for searching a list of data, such as the data in an array. Start by clicking
on the "running man" to open a Replit project called
Searching.
Fork the project so that you have your own copy.
When you open the project, click the plus sign to open a new tab in the
editor and then click directory.txt
to see the file that your program will process.
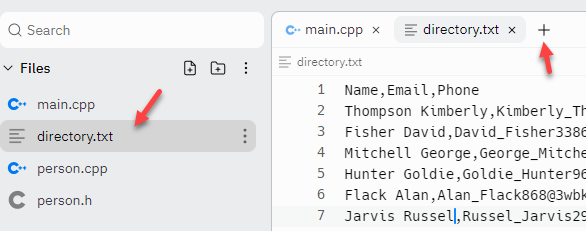
The text file contains a directory of a thousand people, in random order. Each line has three fields: the name (in last, first order), the person's email, and their phone number. Each of the fields is separated by commas.
The Starter Code
The file person.h contains the definition of a Person structure, with name, email and phone data members, as well as the prototypes for some functions and operators.
struct Person{
std::string name;
std::string email;
std::string phone;
};The main() function creates an array of 1000 Person variables, and then calls the load() function to read all of the data from the text file and put it into the array.
const int kSize = 1000;
Person directory[kSize];
load(directory, kSize);Following the array declaration is a do-while loop which asks the user for a last name, and which then calls the find() function to retrieve the record number.
bool done = false;
do{
cout << "Enter the last name to search for (q to quit): ";
string last;
cin >> last;
if (last == "q") done = true;
else
{
int pos = find(directory, kSize, last);
if (pos >= 0){
cout << "\nFound: " << directory[pos] << endl;
} else{
cout << "\nCannot find " << last << endl;
}
}
}
while (! done);If the name is found in the directory, then the program prints out the full name, email and phone number. If the name could not be found, the program just prints "Not found" and allows the user to enter another name. The user can exit by entering "q" when asked for the last name.
The find() Function
Your job is to complete the find() function which searches the array. The function is already stubbed out for you, returning -1 to indicate that the name could not be found. Since the array is in no particular order, your find() function must check each element sequentially, until it finds a match or until it runs out of elements. This is called a linear-search.
Here is the pseudocode (as comments) that you should implement:
int find(const Person contacts[], int size, const string& key)
{
// for each Person p in contacts
// print a . to indicate the progress
// if key == front part of p.name then
// return the index of p
return - 1; // Not found
}Here are some notes on implementing this:
- Because this is inside a function, you can't use a range-based loop, even though I've written the pseudocode comment that way. In fact, since you need to return the index, a counter-controlled loop is more appropriate.
- Printing the "." is not really part of the algorithm, but is going to visually give you an indication of how efficient your search is.
- To compare the key to p.name, you'll need to use substr() and the size of the key in your comparison. Remember, the name data member includes both the last and first names, and you only want to compare against the last.
Linear Search
When you're finished, type make
run in the Console tab, and enter in some last names to search
for. Here's what happens when I run the program.
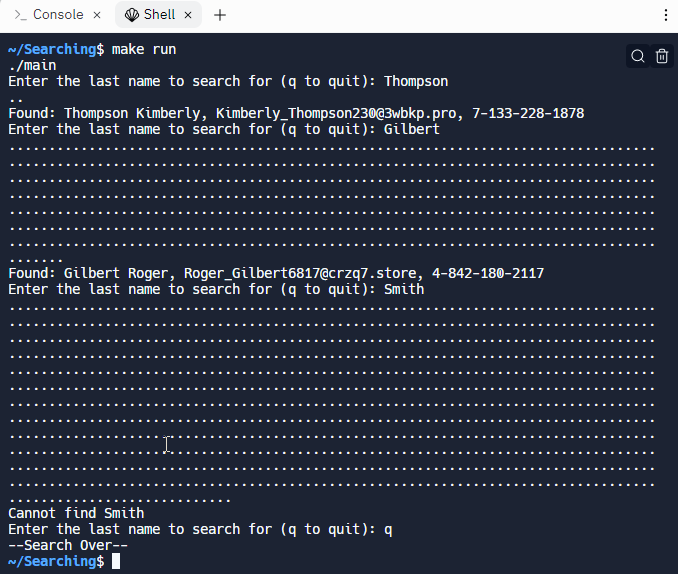
- I start with Thompson, the first name in the file, so the program immediately finds and prints the answer, displaying only two "dots" before the answer.
- When I look for Gilbert, the program needs to look through a little more than half of the array before finding Roger Gilbert.
- When I look for Smith, surprisingly there are no Smiths in the directory. The program has to look through every single element before it can report the fact that it failed.
So, what conclusions can we make from this experiment?
Linear Search Efficiency
One thing that we can tell from this short experiment is that if a name is not in the directory, we'll have to look through all 1,000 names to find that out. As a result, (assuming that the time to compare each name is constant), the running time of linear search grows proportionally with the size of the directory we're searching. If we had a directory of 10,000 names it would be roughly ten times slowerthan our version with 1,000 names.
However, that is the worst case. Most of the time you will find the name you are looking for and won't need to compare all one thousand names.
In the best case, the name you'll decide that you only need to look up Kimberly Thompson, the first name on the list, and your program will seem to run like lightning. On average, though, assuming the names are randomly distributed throughout the directory, you'll have to search through 500 names (or half of the total array) to find the one you want.
In Computer Science we have a particular terminology for discussing the runtime efficiency of algorithms. We say that linear search is an O(n) algorithm, (which mean on the order of n), because the time to find your element increases in a linear manner as the number of elements in the array (n) increases. This is known as Big-O notation.
Even more specifically, we can say that our implementation:
- Has a worst case of O(n). We will always have to search through the entire directory if a name is not found.
- Has a best case of O(1) meaning that if we always search for the first name on the list, we'll find it in constant time.
- Has an average case of (n/2), meaning that on average, we'll find the name by searching half of the the array. Some will be more, some less, but it will average out.
Improving Linear Search
We can improve our algorithm a little bit by putting the data in sorted order. To do that, just call the sort() function which I've supplied, immediately after you've loaded the data, like this:
const int kSize = 1000;
Person directory[kSize];
load(directory, kSize);
sort(directory, kSize);Now, when you run the program and look for Thompson, it is not immediately found, since Kimberly is no longer at the beginning of the list, but much further down. So, that doesn't seem to be much of an improvement.
Remember, though, that before you sorted the data, you needed to check every single element before you could be sure that the name was not found. Now, you can stop whenever the name in the directory is greater than the name you are looking for. Just add this code at the end of your loop do-while loop:
if (contacts[i].name > key) return -1;The average performance time is still O(n / 2), but the worst case time has improved from O(n) to O(n / 2) as well. In general it will take 500 comparisons to see if a name is missing, instead of the 1,000 comparisons you made earlier.
However, this is the best improvement we can make with linear search. To go faster, you'll need a better algorithm.
Binary Search
Algorithm Walkthrough (Video)
Now that you know the elements are in alphabetical order, (sorted), you can adopt an more efficient approach: divide the array in half
and compare the key you’re trying to find (cat in the illustration
below) against the element closest to the middle, using the order defined by ASCII,
which is called lexicographic order.
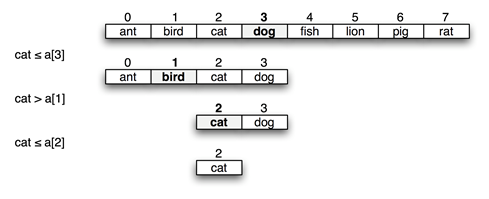
If the key you’re looking for precedes the middle element, then the key—if it exists at all—must be in the first half. If the key follows the middle element in alphabetic order, you only need to look at the elements in the second half.
Because you can discard half the possible elements at each step in the process, it is much more efficient than linear search. Binary-search is a divide-and-conquer algorithm which is naturally recursive.
Implementing Binary Search
Here’s an implementation of binary search, named bfind():
int bfind(const Person data[], int first, int last,
const string& key)
{
cout << "."; // display comparisons
if (last < first) {return -1; } // not found
int mid = (first + last) / 2; // mid point
if (key == data[mid].name.substr(0, key.size())) return mid;
if (key < data[mid])
return bfind(a, first, mid - 1, key); // look in left
else
return bfind(a, mid + 1, last, key); // look in right
}
Add this code before your find() function, and then comment out the body of find(), and add a call to bfind() in its place, like this:
return bfind(contacts, 0, size - 1, key);
Now, when you run the program, you'll see that even the worst case will take
only about 10 or 11 comparisons, instead of 500 or 1000.