Performing a task repeatedly is iteration. Selecting different alternatives is selection. Most of us learn to use the control statements for, while, and if easily, because they are familiar. In this lesson, you'll look at a different, more abstract problem-solving strategy called recursion.

Recursion is a technique where large problems are solved by reducing them to smaller problems of the same form. This is similar to functional decomposition, yet different as well. In functional decomposition, the smaller problems have a different structure. In recursion, the sub-problems have the same form as the original.

To most of us, this does not make much sense when we first hear it. Since it is unfamiliar, learning how to use recursion can be difficult. As a problem-solving tool, recursion is so powerful that it at times seems almost magical.

Recursion makes it possible to write complex programs in simple and elegant ways.

You may be familiar with the notation n!, pronounced "n factorial", the product of all of the positive integers less-than, or equal to n. In mathematical notation it is written like this.

Using a loop, we can implement the function in C++ like this:

int factorial(n)
{
    int result = 1;
    for (int i = 1; i <= n; ++i) { result *= i; }
    return result;
}

Algorithms that use loops like this are iterative. Let's see how to write the function recursively.

Another way to think of the factorial function is as a recurrence relation, which recursively defines a sequence; each further term is defined as a function of the preceding terms.

Without qualification, this is a circular definition. The qualification is that 0! = 1. We can translate this recursive definition into code as well:

int factorial(n)
{
    if (n == 0) { return 1; }      // qualification
    return n * factorial(n - 1);    // recursion
}

The condition (n == 0) is the simplest possible condition. It is called the base case. If n is not zero, then the function multiplies n times the result of (n - 1)!. It does this, by calling itself again to simplify the problem.

The solution to any recursive problem can be organized like this:

If the answer is known then return it          // the base case
If not, then 
    Call the function with simpler inputs     // recursive case
    Return the combined simpler results

This pattern is called the recursive paradigm. You can apply this technique as long as:

1. You can identify simple cases for which the answer is known.
2. You can find a recursive decomposition breaking any complex instance of the problem into simpler problems of the same form.

Because this depends on dividing complex problems into simpler instances of the same problem, such recursive solutions are often called divide-and-conquer algorithms.

The computer treats recursive functions just like all other functions. It is useful to put the underlying details aside and focus on a single level of the operation; assume that any recursive call automatically gets the right answer as long as the arguments are in some sense simpler than the original.

This psychological strategy—assuming that any simpler recursive call will work correctly—is called the recursive leap of faith. Learning to apply this strategy is essential to using recursion in practical applications.

Consider what happens when you call factorial(4); the function must compute the expression n * factorial(n – 1), and, by substituting the current value of n into the expression, you know that the result is 4 * factorial(3).

Stop right there. Computing factorial(3) is simpler than computing factorial(4). Because it is simpler, the recursive leap of faith allows you to assume that it works. Thus, you should assume that the call to factorial(3) will correctly compute the value of 3!, which is 3 × 2 × 1, or 6. The result of calling fact(4) is therefore
4 × 6, or 24.

As you look at the examples in the rest of this chapter,
try to focus on the big picture instead of
the details. Once you have made the
recursive decomposition and identified
the simple, base cases, be satisfied
that the computer can
handle the rest.

In 1202, the Italian mathematician Leonardo Fibonacci experimented with how a population of rabbits would grow from generation to generation, give a set of rules. His rules lead to a sequence of terms, which today are called the Fibonacci sequence: each term is the sum of the two numbers preceding it.

Expressed as a recurrence relation:

This alone is not sufficient, however; you can define new terms, but the process has to start somewhere! You need at least two terms already available, which means that the first two terms in the sequence— t₀ and t₁—must be defined explicitly.

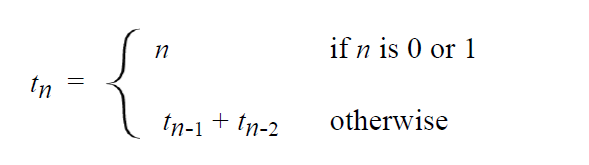
Given this qualification, the Fibonacci sequence can be expressed as:

To write a recursive implementation of a fibonacci(n) function, you need only plug in the simple cases, plus the recurrence relation, and you're done.

int fib(int n)
{
    if (n < 2) { reture n; }     // base case
    return fib(n - 1) + fib(n - 2);
}

How do you convince yourself that the fib() function works? If you begin by tracing through the logic, I guarantee that you'll be confused. Instead, regard this entire mechanism as irrelevant detail.

Since the argument values are smaller, each of these calls represents a simpler case, and so, applying the recursive leap of faith, you can assume that the program correctly computes each of these values. Case closed. You don’t need the details.

So, how efficient is the fib() function? What we mean by that is, how much memory does it use and how fast does it run? (Those are called the space and time measures of efficiency.) You can get a quick idea by simply calling fib(42). It seems to take forever! Why?

This particular recursive implementation of fib() is extremely inefficient, because the function makes many redundant calls, calculating exactly the same term in the sequence several times. Given that the Fibonacci sequence can be implemented quickly and efficiently using iteration, this is more than a little disturbing.

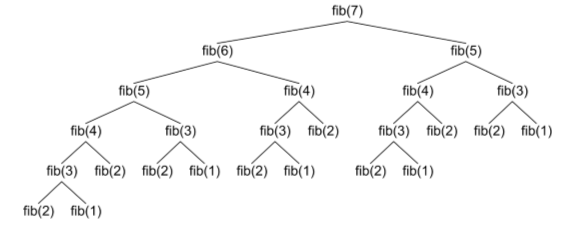
The problem here is not recursion, but the naïve way in which is implemented. In this case, we are repeatedly calculating the same value. By using a different strategy, we can write a recursive version of fib() where all of these redundant calls disappear. You’ll learn how to do that in the next lesson.