There are two kinds of control statements: selection (decision) and iteration (loops). Selection is also called branching, because any time you run the program you may take a different path through the code. C++ has the same five branching or selection statements that you met in Java.

Let's start with the if statement which is the simplest conditional statement in C++.

if (condition) { statements }
if (condition) statements else statements

Use the first form when you want to carry out an action when condition is true, but do nothing when it is false. This is known as a "guarded action" pattern.

Use the second form choose between two mutually-exclusive actions. This is the either-or version of the if statement; the "alternative action" idiom or pattern.

Here's an alternative-action example which tells if an integer n is even or odd.

cout << "The number " << n << " is ";
if (nt % 2 == 0)
{
    cout << "even." << endl;
}
else
{
    cout << "odd." << endl;
}

In previous example, both the if body and the else body contain a single statement, so braces are not required, even though I would recommend adding them. When you want to have a group of statements in place of a single statement, place those statements in a block, sometimes called a compound statement, which is a collection of statements enclosed in curly braces.

The placements of braces and indentation are topics of "religious" fervor. You can read more about the "wars", and the different styles on Wikipedia.

The most common styles are K&R style, which places the opening brace on the same line as the header, and Allman (or ANSI or BSD) style, which places the opening brace on its own line.

// K&R Formatted
cout << "The number " << n << " is ";
if (nt % 2 == 0) {
    cout << "even." << endl;
} else {
    cout << "odd." << endl;
}

The K&R style, shown here, is more compact, but, for me, the Allman style (which is what I normally use), is more readable.

Statements inside of a block are usually indented. The compiler ignores the indentation, but the visual effect is helpful since it emphasizes the program structure when reading it. Empirical research has shown that indenting three or four spaces at each new level makes the program structure easiest to see; in CS150 I'll use four spaces for each new level.

Indentation is critical to good programming, so you should strive to develop a consistent indentation style in your programs.

The if statement tests a condition, an expression whose value is either true or false. This is called a Boolean expression, after the mathematician George Boole, who developed the mathematical theories which underly much of Computer Science. In C++, the built-in Boolean data type is called bool.

You can create bool variables, just like other variables:

bool a = true;
bool b = false;

A Few Pitfalls

In Java, the bool type is called boolean, while in Python, the values are capitalized, as True and False. However, those are minor differences. The real pitfalls with the C++ bool type is that, for historical reasons, the bool type implicitly converts to many other types. This is not true in Java or Python, so it may be a source of confusion for you.

When the C++ compiler needs a Boolean value (such as in a an if statement, or a while condition), and it finds a value of another numeric, pointer or class type then:

1. If the value can be converted to 0 then it is treated as false.
2. Otherwise, the value is treated as true.

bool a = 5;           // 5 converted to true
int b = a;            // a converted to 1
bool c = 0;           // 0 converted to false
bool d = "hello";     // "hello" (a pointer) converted to true;
cout << d << endl;    // prints 1 (NOT true)

You'll notice that printing the bool variable d in this example does not print true or false as it would in Java and Python, but 1 and 0. You can change that by using the boolalpha manipulator, like this:

cout << boolalpha << d << endl;

We'll revisit the effects of this behavior as we go on. You can run this example in an online IDE by clicking the link in this sentence.

The six relational operators are all binary operators which compare two values and return true if the relationship holds between the two, and false otherwise. Assume we have these variables:

int a = 3, b = 5, c = 2;
string s1 = "sam", s2 = "mary";

Here are the six operators. Each condition listed here is true.

• Equals: ==. if (a == b - c) ...
• Not-equals: !=. if (a != b) ...
• Less-than: <. if (s2 < s1) ...
• Less-than-or-Equals: <=. if (a <== b - c) ...
• Greater-than: >. if (s1 > s2) ...
• Greater-than-or-Equals: >=. if (b >== a + c) ...

Relational operators compare primitive types, but they also work with many of the types supplied by libraries, such as string and vector. Again, this is different than Java, where you have to use equals() or compareTo() to compare String objects.

More Pitfalls

As in Java and Python, the equality (==) operator uses two = symbols.; a single is the assignment operator. Unlike those languages, accidentally using a = when you mean to use == creates an embedded assignment, which is legal, not what you expect.

if (area = 6) ... // always true

This would be a syntax error in Java or Python. In C++ it assigns the value 6 to the variable area, and then, when the condition is evaluated, converts that 6 to true.

Comparing floating-point numbers is legal (syntactically) using the relational operators, but it is also problematic. (This is actually true in any programming language; it's not unique to C++.) For instance, the following expressions evaluate to false, not true, even though they are both mathematically true:

1.0 == .1 + .1 + .1 + .1 + .1 + .1 + .1 + .1 + .1 + .1; // false
sqrt(2.0) * sqrt(2.0) == 2.0;  // false

These occur becuase of representational errors in binary numbers. Just as the number 1/3 can't be exactly represented in base-10 (decimal), many numbers cannot be precisely represented in base-2 (binary). When you do calculations with these numbers, those small errors are magnified, and you end up with nonsensical comparisons such as these.

In addition to the relational operators, C++ defines three logical operators that take Boolean operands and combine them to form other Boolean values:

Logical Operators
! or not	Unary NOT (true if its operand is false)
&& or and	Binary AND (true if both operands are true)
|| or or	Binary OR (true if either or both operands are true)

In C++ you can use either they operators &&, ||, and ! as you would in Java, or the English words and, or, and not, as you would in Python.

Use the logical operators to combine multiple conditions like this:

if (percent >= 6.25 && percent < 78) { grade = "C"; }

Here, both conditions must be true for grade to be set to "C". Here's another example:

if (c == 'a' || c == 'e' || c == 'i' || c == 'o' || c == 'u')
{
    result = "vowel";
}

Here, result is set to "vowel" if any one of the conditions is true.

Short-circuit Expressions

When C++ evaluates an expression with the logical operators:

• the sub-expressions are always evaluated from left to right.
• evaluation ends as soon as the result can be determined.

For example, if expr1 is false in the expression expr1 && expr2, there is no need to evaluate expr2 since the result will always be false.

Similarly, with expr1 || expr2, there is no need to evaluate expr2 when expr1 is true.

In both of these cases, evaluation which stops as soon as the result is known. This is called short-circuit evaluation.

Often, your programs will need to handle many different conditions: in one case, you should "turn left", in another you should "turn right", while in a third, it should go "straight ahead". When you have more than two branches, there are three general techniques to use:

• Sequential if statements should be used when each test depends on the results of a previous test. The tests are performed sequentially.
• Nested if statements are used when the calculations or actions you need to carry out depend on several different conditions, of different types.
• switch statements allow you to easily write "menu style" code. You can place each action in a block (called a case block), and directly jump to (and execute) that block whenever the user enters the appropriate selection.

One sequential comparison which you're all familiar with is the "letter grading scale" used to assign marks in school, (including in this course), similar to that shown here:

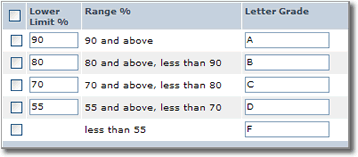
Typically, your letter grade is based on a percentage representing a weighted average for all of the work you've done during the term. To select one course of action from many possible alternatives (which is the case here), you employ sequential if statements following this pattern:

if (condition-1)        // condition-1 is true
  statement
else if (condition-2)   // condition-1 false, condition-2 true
  statement
...
else if (condition-n)   // conditions 1-n false, condition-n true
  statement
else                    // if no conditions are true
  statement

This is called the "Multiple Selection" pattern. It is also known as a "ladder style" if statement, because each of the conditions are formatted one under the other, like the rungs on a ladder.

Another way to code multiple-alternative decisions is with nesting. Nesting means that one if statement is embedded or nested inside the body of another if statement, much like the traditional Russian nesting dolls.

Use nesting when you have different levels of decisions. For instance, if you're one of those fortunate folks making more than a hundred thousand dollars a year, you calculate your taxes using the following formula, instead of using the tax tables:

First locate the schedule for your filing status (Single), then find your income bracket. Use a set of sequential if statements to determine which set of calculations to use. Then, nested inside the body of each portion test the income levels, like this:

if (status == kSingle) // calculate single
{
  if (income <= kSingleBracket_1)
    tax = income * kSingleRate_1 - kSingleEx_1;
  else if (income <= kSingleBracket_2)
    tax = income * kSingleRate_2 - kSingleEx_2;
  else
    tax = income * kSingleRate_3 - kSingleEx-3;
}
else if (status == kMarriedJoint)  // married filing jointly
...