The naïve version of the recursive Fibonacci function which you met in the last lesson was very inefficient. As the numbers get larger, it takes an increasingly large amount of time to generate each one. This is because for each number we find, we have to generate all of the Fibonacci numbers preceding it.

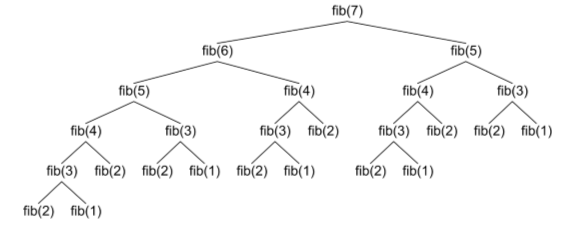
In Computer Science, we say that this implementation has an exponential, or O(2ⁿ) runtime performance; as n gets larger, we double the number of calculations at each step. That means that it could literally take years to calculate a Fibonacci number of even a moderate size using this function.

We can reduce those years to a fraction of a second by learning about wrappers and helpers. A wrapper is a non-recursive function that calls a recursive function. A helper is the recursive function that the wrapper calls. Let’s apply that to the Fibonacci sequence.

We can instantly calculate fib(n) when we know the values of fib(n-1) and fib(n-2). When you don’t know those values, the calculation takes a lot of time, but when you do, then it’s really fast.

Are there values for fib(n-1) and fib(n-2) that we do know? Let’s write out the sequence and see:

n	0	1	2	3	4	5	6	7	8	9	10	...
fib(n)	0	1	1	2	3	5	8	13	21	34	55	...

Since fib(0) is 0 and fib(1) is 1, we can start there. For our recursive helper, just write a function that accepts n and the two terms: t0 and t1. If n is 0 return t0 and if it is 1, return t1. Otherwise call the function recursively with n - 1.

When calling the function recursively, however, instead of passing the t0 andt1, calculate the next two terms and pass those instead. Here’s what the helper should look like:

int helper(int n, int t0, int t1)
{
    if (n == 0) return t0;
    if (n == 1) return t1;
    return helper(n - 1, t1, t0 + t1);
}

For the fib() wrapper function, just call the helper, kick-starting it with the first two terms, 0 and 1. Here’s what the function looks like:

int fib(int n)
{
    return helper(n, 0, 1);
}

A palindrome is a string that reads identically backward and forward, such as "level" or "noon". Although it is easy to check whether a string is a palindrome by iterating through its characters, palindromes can also be defined recursively.

Any palindrome longer than a single character must contain a shorter palindrome in its interior. For example, the string "level" consists of the palindrome "eve" with an "l" at each end. Thus, to check whether a string is a palindrome—assuming the string is sufficiently long that it does not constitute a simple case—all you need to do is

1. Check to see that the first and last characters are the same.
2. Check to see whether the substring generated by removing the first and last characters is itself a palindrome.

If both apply, then the string is a palindrome. So, what are the simple or base-cases? A single-character string is a palindrome because reversing a one-character string has no effect. The one-character string therefore represents a simple case, but it is not the only one. The empty string—which contains no characters at all—is also a palindrome.

Here is a recursive function which returns true when given a palindrome.

bool isPalindrome(const string& str)
{
    if (str.size() < 2) { return true; }     // base case
    return str.front() == str.back() && 
        isPalindrome(str.substr(1, str.size() - 2));
}

If the length of the string is less than 2, it is a palindrome. If not, the function first checks to see that the first and last characters are the same, and, if they are, it calls itself again with a shorter substring, removing the first and last characters from str.

Like our original,naïve fibonacci function this implementation is also very inefficient, but for a different reason.

• The fib() function was inefficient because every time we calculated a term, we first had to (re)calculate all of the lower terms. It was expensive in terms of time.
• The isPalindrome() function is inefficient because every time we enter the recursive call, we first have to create a new substring, which not only takes time, but also uses extra memory. This function is expensive in terms of space.

We can improve the performance by making these changes:

• Calculate the size of the string only once.
• Don’t make a new substring on each call.

The main inefficiency is the repeated substr() calls. You can avoid this by passing indices to keep track of the positions instead of creating new substrings.

Of course, that means we'll need a helper and a wrapper. Here they are:

bool palHelper(const string&, int i1, int i2)
{
    if (i1 >= i2) { return true; } 
    return str.at(i1) == str.at(i2) &&
        palHelper(str, i1 + 1, i2 - 1);
}
// Wrapper
bool isPalindrome(const string& str)
{
    return palHelper(str, 0, str.size() - 1);
}